Integro-differential equation

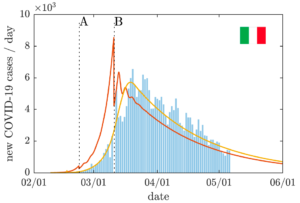The spread of COVID-19 at the end of 2019 with its delay properties requires improved dynamical models to forecast and evaluate specific measures in politics. As these policy measures require real-time information on the evolution of the diseases, quantities like delay due to incubation time and infectious period can not be neglected and need to be modeled in detail. This is why we revive in this work a model which had been introduced by Kermack and McKenrick in 1927 and which is based on a time-dynamical system of integro-differential equations. It is capable of integrating past infection events into the present infection rate and is a generalization of the well-known and broadly used compartmental ordinary differential equation models. The proposed model is generalized, carefully analyzed for its (mathematical) properties and studied particularly in the application on COVID-19. It is worth mentioning that testing the model on disease evolution data available, one can observe a very precise fit of the evolution. With the help of this model, the effect of restrictions for shelter in residence and similar measures — including age dependent restrictions — and their delayed response in the reported data on the number of people infected can be studied in detail. We formulate and solve related optimal control problems, which reveal for instance that immediately before reaching herd immunity, it is advisable to significantly increase contact restrictions. This makes it possible to completely stop the spread, preventing it from continuing until most of the population has been infected or is immune. In general, the model class presented here can answer many relevant policy questions with a significantly higher degree of precision than original compartmental models and therefore constitutes a preferable model.

Link to preprint: Prepint on ResearchGate

Alexander Keimer, Lukas Pflug